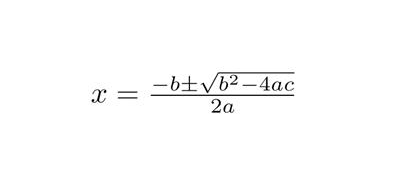What to Expect to See in Algebra 2

The algebra 2 math is found in 13 different chapters and every chapter had been divided into many lessons. Within every lesson, there is theory and examples of solving such problems.

• Functions: before you learn about anything else, it is good if you learn how to combine the functions with the arithmetic operations and composing of the functions. You should learn about transforming function in a way that shifts, reflect or stretch the graphs. It is also the time to learn the inverse functions and how you can get to them.
• Complex number: With this chapter, you get to know about the complex number, the way of adding, subtracting and also multiplying each number.  This can be useful when it comes to working for the polynomials.
• Arithmetic using polynomials: you should learn about adding, subtracting, multiplying and dividing the polynomials.
• Polynomials: you can learn how you can manipulate the polynomials so that you can prove their identities and to find the zeros on such polynomials.  The knowledge may be used in order to solve the polynomial equation with the graph polynomial functions. It is time to learn about the symmetry of the functions.
• Radical relationship: in the topic, you learn about solving the radical equation and they are an equation that has the radical expression with them and avoiding having an extraneous It is time to learn about graphing of the radical functions.
• Rational relationship: the rational expression are the same as the fraction, however, in the place of using integers within the numerator or the denominator, there is the variable expression. This is the time to learn the method of using these expressions such as dividing, multiplying, subtracting, adding and simplifying. After this, it is time to solve the equation that has rational expression within them and to analyze their behaviour using rational functions.
• Exponential growth with decay: it is time to learn about analyzing and manipulating the exponential functions with the expression so to study the rate they use in changing.
• Logarithms with exponentials: you may learn about the logarithms since they are the inverse of the exponents. You may use the logarithms in order to solve differential equations and to analyze exponential and logarithmic functions with the graphs.
• Trigonometry: it is time to learn the definition of basic trigonometric function and how to use the advanced trigonometric function in  many ways.
• Advanced equation with functions: this is a chapter that teaches more about solving equation through graphing. It is easy to interpret the advanced features of the functions such as periodicity, end behaviour and symmetry according to its context and then to compare such features in different functions.

Tips on How to Solve Algebra Problems

By using the multiplication table, it is easy to come up with the number that it is given as a variable. When solving the algebra problem, then you will have to figure out the value of the x and other variables which makes a statement given to be true or which satisfies such equation.

If the solution to the equation is easy to see, then it is easy to use mental patterns or mental math to do it. Most of the time, the equation may be harder in solving and in this case, it is important to simplify an equation before solving such problem.  One method used in solving such problem is using inverse operation. The operation will need to use subtraction, division, multiplication and addition. The inverse operation works with the operation which may reverse an effect of a new operation. The subtraction and addition may work as the inverse of one another, like the multiplication and the division are also inverse.

algebra problem

Most of the time, the student does not like the idea of working on an algebra problem, and most of the time the reason for this is that they fail to understand which steps to take and what the problem has been all about.

For the student to solve the problem, he should start by understanding what variable in the equation is being asked to find the answer for. Knowing the correct variables of the equation is the first step to identify which system to be used afterwards. The student should then use an equation which is constructed within the part C in order to solve the equation of X. To be able to do this, it is good if the student is aware of how he can solve differential equation problems.

A process used in finding out which type of the variables that make the equation to be true, is through solving the algebra problem. To get the answer, it is good to add, to divide or to multiply the two sides an equation using the variables or numbers. This will help to get one variable on one side of a single number to another side.

By doing the same thing on the two sides of an equation and by doing the operation in the right order, then the solution will be gotten. By just looking at the equation, then it is easy to come up with the right order to follow.

By solving algebra problem, it is good to keep in mind that all the answers may not be the best integer. Even if the answers are kept simple, they are not always that so it is good to be open to the answer that you may get after solving the problem. You should not think that there is a mistake by not getting a straight answer.

How to solve quadratic equations using completing the square method?

Quadratic equation can be solved using factorization method, completing the square method and quadratic formula method. In this module we will study the ‘completing the square method’.

Solve the quadratic equation, using the ‘completing the square’ method. Follow these steps:

• Step 1. Make the coefficient of x2 unity (i.e., 1)
• Step 2. Take the coefficient of x, now divide it by 2, now take the square of this value, the result obtained should be added and subtract in the original equation to maintain the original value of equation.
• Step 3. Take the x² term, the x term and the constant (that you just added and subtracted) to form the perfect square. Using the identity (a+b)² = a²+b²+2ab
• Step 4. Take the remaining term on the right hand side
• Step 5. Take the square rot on both the side.
• Step 6. Do not forget to take both positive and negative sign. Because square of both (+x) and (-x) is (x²)
• Step 7. Simplify the equation; transfer the constant term to right hand, taking positive and negative sign one by one.
• Step 8. In this way you will get two values of quadratic equation

Let us take a numerical example to understand this method in a better way:

Let us take the original quadratic equation to be 2x²-7x+6=0

Now make the coefficient of x² unity (i.e., 1)

The equation will become

The equation simplify to

Now let us take the coefficient of x, that is  now take half of it, , now do the square of this value, it would become , now add and subtract  in the above equation

Now rearrange the equation as

Now since   is equivalent to  because of identity

Now our equation simplifies t

Now transfer the constant term on right hand side

or

or

Now taking the square root on both the side

Now there are two cases

Case 1: taking positive sign

or

Case 2: taking negative sign

or

To build a command on this method, try to practice as many questions as possible.

Try following algebra homework

Question 1.

After solving question 3 you will realize, you face square root of a negative number. It is called iota and it I beyond the concept of normal algebra. T is dealt in greater detail in complex number and complex algebra.

Sometimes when there are so many equations to solve, or when people find it too difficult to solve colossal number of mathematical equation then mathematician have come up with expression calculator.  This software helps in solving difficult algebraic expression within seconds.

Good students not only work hard, rather they do it smartly. To understand the concept of math in a better way, one must access to various algebra software. The best mathematics calculator allows a person to perform wide variety of mathematical calculation. Hence, learning mathematics becomes fun.

Complete guides to algebra help for solving quadratic equations

Are you not able to solve the quadratic equations? They do not worry because here you will get a remedy that let you solve the problems very easily. It is known as the algebra help that has helped millions of students all over the world with interactive and effective programs. The algebraic software is best for providing the lessons and worksheets that let the student to build concepts and foundations regarding the topics. Also, the students can solve the problems of a different form that will increase their confidence regarding the topics. Know what is an algebra help and about it.

Algebra help:

This consists of mainly three sections that let the students and teachers master in the field of algebra. The three sections are-

Lessons– here the students will learn all the algebra related topics such as are simplifying the equations, finding the common factor, factoring and solving the equation using the quadratic formula. The lessons are not only interactive, but they explore the vision of students and help them to deal with the dozens of problems. They will get to know about the different categories of problems that can be asked in the future examinations. Given below the list of topics that the lessons cover:

Equation basics– This topic deal with the definition of the algebraic equation and how the equation is formed. They will get to know about the symbols used to represent the variables and coefficients.

Properties of algebra– You will get familiar with all the major properties of algebra that is essential to solving the problems. Some of the important properties are commutative, cumulative property.

Simplifications– you will learn how to simplify any equation and find the common factor for the equation. How multiplication of two binomials will give the solution to the problem using the FOIL methods are also covered in the topics.

Calculators- Have you heard of the equation calculator? An equation calculator helps to reach the correct answer using simple and easy steps. It had built and updated over the years so that it can precisely find the solutions. The list contains finding factors for the given equation, completing the squares, expressing the equations in factors, functions using the calculator and other methods. The calculator is capable of solving equations of the order of 15 million. The easy and step-by-step calculators help to reach correct solutions.

Worksheets– If one knew how to solve the quadratic equations using the formula but had never practiced other forms of quadratic equations then he will find problems to solve other forms of equations. Worksheet overcomes this major problem that usually most of the student do, it let the student solve new and fresh problems that will help them to build strong concepts. After one has attempted questions, they can check their answer using the answer key. The worksheet solution key contains a detailed step-by-step solution for the problem.

If one wishes to avail the benefits of algebra help, then they should know about it in brief so that they too can solve the problems without distractions. You too can be the master algebra and get good scores in exams.

What is a Factor and how to Find Factors?

A factor:  The complete set of whole numbers called factors. When you will multiply one number by the neighbor number of the set, you would get the factoring number. Such as the number 3 has two factors 1 and 3 and the number 8 has four factors 1, 2, 4, and 8.  Which factor contains negative numbers called integer factors. In that case 3 has four factors: -3,-1, 1, and 3. 8 has 8 factors: – 1, -2, – 4, -8, 1, 2, 4, and 8. 1, 2, 3, 4, 5 are the natural numbers. There is not any fraction of the natural number. From 0 to infinity all whole numbers are natural numbers. Integers are also natural numbers with including negative counterparts. It is not so difficult how to factor numbers with the natural numbers. You can find at least two factors in any number.

How to find factor from the natural number:

If you want to find a factor of any number, then you will start to divide it. Without the number 9, you can continue dividing numbers until it reached into 2. When you do not find any rest that means both are divisor and the remaining common quotient are its factors. Now, look at the number of 9. It is divided by 3 and 1 but not divided by two. The factors of 9 are 1, 3, and 9.

For the integer set, you need to add negative equal numbers to your results. Such as 9 have the integers set is -9, -3, -1, 1, 3, and 9. There is only one integer that has infinite factors. This integer is zero. One is the only number which has zero as a factor.

Factoring in an expression:

An algebraic expression carries some number which called coefficient, variables, and constant.

In the expression x² + 4x + 8, where 1 is the coefficient of x². 4 is the coefficient of x, and the constant is 8. A constant is not multiplied by a variable. When the power of a variable is 0 then it will be, x⁰=1.

For factoring an expression, we need to collect the Greatest Common Factor (GCF). In the expression collect the factors of every component.

Take this equation x² + 4x + 8, it has factors look bellow

X²– 1

4x- 1, 2, 4

8- 1, 2, 4, 8

In that equation, we find only the common factor is 1. It has no coefficient greater than one. Look another expression that is

2x³+ 16 x² + 6x. Its factors are

X³-1, 2

X²– 1, 4, 2, 8, 16

x- 1, 2, 3, 6

Here we find the common factors are 1, and 2. Now multiply two with the variable x we find 2x. Divide every component in the expression by 2x.

2x³/2x = x2

16 x²/2x= 8x

6x/2x = 3

Now we find the GCF how to factor out. That is

2x(x² + 8x + 3).

How to find factors of a binomial expression:

Which expression has two terms of a variable is calling binomials. 2x²– 6x is a binomial expression. From this equation, we look the GCF factors are

2x(x-3). (X-3) has no any factor.

Different Ways of Subtracting Fractions

When it comes to subtracting fractions, it is important to learn how to subtract the fraction using unlike and like denominators.  You can subtract the mixed number using or not using regrouping, solving of the application problem which is required for the mixed and fraction numbers.

In some cases, the subtraction and not the addition, it will require someone to solve the problems which involve the fraction.

The easier way of doing simple fraction subtraction problem is for these that have two proper fractions that have a common denominator.  This means that every denominator works the same. The process is an addition of the faction like the denominators but expects when using the subtraction.  In this case, it is easy to subtract the second numerator away from the first one while keeping denominator to be the same.

Subtracting Fractions

If a denominator is not the same also called unlike denominators, then a person should rewrite a fraction using a common denominator. By using least common denominator also known as least common multiple denominators, it will be a most efficient choice.  However, any common denominator may be used. You should check the answer if you want to be sure that you have used the simplest form.  Use a prime factorizing when you want to find least common multiple.

Subtracting the mixed number

Subtracting the mixed number, it does work in same away like adding the mixed number. The first step is subtracting whole number part of a mixed number, then subtract the fraction parts of mixed numbers.  Afterwards, the whole number will be combined while the answer will be in a fraction in order to express the answer of the mixed number.  Sometimes, it can be easy to use the mixed number like improper fraction before solving.  When needed,  you may have to find the common denominator if you would like to solve the subtraction problem of the mixed number.

Subtracting the mixed number using the regrouping

Sometimes, if you subtract the mixed number, fraction part of a second mixed number which is larger compared to the fraction of the first number.  As it happens with many fraction problems, you may need to get the common denominator.  You should keep in mind that a key to add or to subtract the fraction with the mixed number is through making sure that there is a common denominator at the beginning. The original fraction will not do not have the same denominator.  You should get one if you want to continue to another step.

There are times when the mixed number may be subtracted using the whole number. In such case, you will have to write the whole number like a mixed number so that you can do the subtraction. You may use the equivalent mixed number which has one denominator like the fraction of mixed number.

When the fractional part of mixed number which has to be subtracted looks larger compared to the factional part of the mixed number form that should be subtracted or if the mixed number has to be subtracted, then you will have to subtract 1 away of the whole number of mixed number which should be subtracted and then add 1 at the fraction part so that you can make the improper fraction.

Learn How to Solve Quadratic Equation – Factorization or Equation Calculator

Most basic question is what is quadratic equation? The answer is, any algebraic equation having degree two with its coefficient, is called quadratic equation.  The quadratic equation is one of the most complex equations of the mathematics where a student feels complexity in solving them. It is easy to solve any linear equation, but it is quite tough to solve an equation with a higher degree.

Quadratic Equation

How to solve quadratic equation?

To solve any quadratic equation there are two methods one is the most basic method which is also known as formula method, another method is directly used quadratic equation calculator.

Method-1: Factorization

Firstly, let us discuss basic method which is quite easy to understand.

The standard form of quadratic equation is –

ax²+bx+c=0

Let us consider an example, a.) x² + 4x +3=0

Apply basic factorization method to solve this equation.

Step-1) x(x+3) +1(x+3)

Step-2) Arrange common terms together

Step-3) (x+1) (x+3)

Step-4) x=-1 or -3

For better understanding, let us consider another example, b.) x²+5x=0

Step-1) take x in common

Step-2) x(x+5) =0

Step-3) x=0 and x+5=0

Step-4) x=0 and x= -5

Therefore, x has two values, x=0; x= -5

Method-2: Quadratic equation calculator

Now, we discuss another formula to solve quadratic equation, which is known as quadratic equation calculator.

To solve the quadratic equation, the algebra calculator uses a genuine method or use a formula to identify values of a variable. The formula for solving quadratic equation is

x= (-b±√ (b²-4ac))/2a

Let us consider an example,

x² + 4x +3=0

So, here a=1, b=4, c=3, now put all these values in the above equation, then solve it.

Therefore, you got two values of x, x= -1 or x= -3.

It is a direct formula-based method, or the digital calculator offers their users to solve any of the quadratic equations with the formula method. That means you can learn how to solve any quadratic equation with the formula method. In the calculator, you just need to enter the question in the required field. Different signs, roots, square root, and mathematical signs are available on the platform. Thus, you can enter the quadratic equation to solve it and find its variable values. According to the degree available in the unknown term, you will get values accordingly.  Now a day, the quadratic equation is also available on the internet where one can direct put values in the given space and then click on the submit button to get the final value of your required coefficient.

Here, you can choose the algebra calculator that can easily find out variable values and deliver results in fast. In the algebra calculator, you just need to enter the quadratic equitation on the required field in the calculator. Thus, enter one next tap to solve the equation. The calculator solves the equation with the genuine method, and there is no short answer you will get. Thus, solving quadratic equations is quite easy with the calculator as compare to factorization method. Factorization method sometimes fails in solving an algebraic method only when the equation is of higher degree, which makes the solution too much complicated. In that case, quadratic equation calculator method is beneficial for the user.

If someone is comfortable in factorization then apply, factorization method to solve quadratic equation otherwise use easy to implement a method which is quadratic equation calculator.

A Brief Introduction to Quadratic Equation

Do you know about Quadratic equation? If your answer is “No” Then we will tell you the answer. A quadratic equation is an algebraic equation where coefficients with a degree of two or more. A standard quadratic equation contains only the powers of a coefficient of X, which are non-negative. But how to solve these equations, if you are unaware then here is the way. After this, you will be able to solve any question of quadratic equations.

How to solve a quadratic equation?

To know the exact method to solve the quadratic equation, read this article. Consider an example of a quadratic equation which helps you to understand their solution

x² – 5x = 6

The standard format of quadratic equation is-

ax² + bx + c = 0

According to the standard format of quadratic equation, the given an example is not as the standard format. Thus, you need to make the R.H.S. is equal to zero of the above example. You will get-

x² – 5x – 6 = 0

The standard format of quadratic equation, you have

a=1, b=-5 and c=-6

To solve the given quadratic equation, you need to use the Quadratic formula calculator that can help you to perform complex mathematical operations easily. The quadratic formula is

x = (-b±√ (b²-4ac))/2a

The quadratic equation solver teaches you to solve any problem. Once you entered the problem into the required field in the calculator, it explained each step of the quadratic solution. In the solving process-

Puts the values in the quadratic formula

x = (-(-5)±√(25+4.1.6))/2.1

x = (5±√ (25+24))/2

x = (5±√49)/2

x = (5±7)/2

Now, you have the result of the given problem. In the quadratic equation, there are two results you can find that means; you will get two factors for a single variable. So, you need to separate ± signs and find both values of a variable.

If you consider positive sign then the answer will be:

x= (5+7)/2

x=12/2

x=6

If you consider negative sign then the answer will be:

x= (5-7)/2

x= (-2)/2

x=-1

Now, you have two values for single variable, i.e. x=6 and-1. Therefore, X=6 and -1.

The algebra is the most important branch of mathematics that includes the higher degree of at least one coefficient. The higher degree of the coefficient in the equation improves the complexity of the equation which becomes a nightmare for the students. A Linear equation is quite easy to solve, but any equation with the higher order of degree is too difficult to solve. For solving such kind of equation, one can also use quadratic equation calculator, for instant results without any complex calculations.

The digital calculator offers their users to solve any of the quadratic equations with the formula method. That means you can learn how to solve any quadratic equation with the formula method. In the calculator, you just need to enter the question in the required field. Different signs, roots, square root, and mathematical signs are available on the platform. Thus, you can enter the quadratic equation to solve it and find its variable values. According to the degree available in the unknown term, you will get values accordingly.

For example- In a linear equation, there is single degree available in the variable thus you will get one answer for the unknown variable. On the other hand, the quadratic equation includes 2nd order degree that delivers two values of unknown.

If someone is comfortable in factorization then apply, factorization method to solve quadratic equation otherwise use easy to implement a method which is quadratic equation calculator.

Solving the Quadratic Equation

In the wide varied domain of algebra, we come across various kinds of math problems involving the need to solve them. These things termed as equations are further classified into multiple parts. Some of them are Linear equations, Quadratic equations, Cubic equations, and Polynomials.

An algebraic equation with the maximum order of the variable being two is a quadratic equation.

Let us start with understanding the form of the quadratic equation.

Something of the form ( ax² + bx + c = 0 )is a quadratic equation.

Here the letters a,b and c are the coefficients of the equation.

math

It is important to know what exactly the solution of an Algebraic equation means.

To find the solution of an equation, we equate the function or the equation to zero and further solve with respect to that condition. Now that we have known what a solution means in the mathematical terms

Let us know how to find the solution.

The solution of a quadratic equation can be found out using three methods, which are listed below.

1. Factorizing the Equation

The very first method is the factorizing method. It is the most used and easiest way to get the solutions in a very accurate and reliable manner.

Let us know what factorizing is:

It is basically about dividing the coefficient that belongs to order one, into products of two numbers such that it is equal to the coefficient of the 1^st order of the variable. It is a very useful skill that is applicable in many algebraic problems.

After separating the numbers, present them using the distributive property of multiplication which is of the form (x+a)(x+b) where a,b, can be any numbers and x is the variable.

Once you have learned the art of factorizing, the further processes are very basic and trivial. Now to find the solution, as previously discussed, equate each bracket (x+a) and (x+b) to zero. You will find the values of x in terms of the solutions as –a and –b respectively.

This can be further mastered by practicing a small problem set of examples.

2. The Quadratic Formula

You can always try for the factorizing way first, but if in case you are stuck somewhere or if the factorizing gets tough, or the answers are complex, you have no choice but to remember this method. No worry, it isn’t a huge gigantic formula but a little act of remembrance that will help you lifelong in solving quadratic equations. This is the most effective way that will surely lead you to the right answer.

math

Here the value (b² – 4ac) is the discriminant. This value of the discriminant further helps to categorize the nature of the roots.

If the value of the discriminant is positive, then the equation has 2 real solutions, if the value of the discriminant is zero, then the equation has one real and one complex solution. If the value of the discriminant is negative then both the roots are negative.

Even if you use the factorizing way but aren’t sure about your answers, you can give this method a try, just to verify your derived answers. It is very beneficial in solving large and complex equations.

3. The Smart Calculator

Nowadays, you do not have to worry if you mess up with a few steps. If you still do not feel confident about the answer, give the computer processor a try! Try solving the problem using an Algebraic calculator, and you no more need to verify it!

Getting difficulty in Solving Polynomial Expression, Use Online Math Software

Are you a high school student? Then definitely you have some favorite subjects, it could be science, mathematics, English or any other. Learning your favorite subjects will not make you stress, and you are always ready to study it. Learning them is fun and exciting, and you never feel bored. Not all subjects are interesting, and mathematics is not the favorite of many students. It is not tough when you are in the lower grade, but as you move to the higher class, you have to solve difficult problems like polynomials, algebra and multiplying fractions.

polynomial

Many students face difficulties in explaining them, and that’s why their parents hire tutors. But hiring a tutor is not the best option because he will also teach the same way the student learns in school. Spending extra hours in learning mathematics will help you, but what if you are stuck in between solving the problem and there is nobody to help you at that moment. At that time you can take help of online math software that can solve complicated equations within seconds. This software is useful for students and helps them in examinations.

What can you do with online math software?

• Students can solve any algebra problems; solve any polynomials expression, etc.
• Learn step by step operations to solve the equations. Simplify each problem in straightforward ways that even a weak student can understand it.
• Students can see the online demo and watch the tutorials according to topics. All the topics are listed in the table and students can watch the latest and previous solved questions by watching videos.
• While solving any equation say polynomials expression you stuck at any step then use the online software. Just enters the whole expression and press simplify to get the solution.
• Learn how to apply the rules to solve the particular problem.

Taking help of internet in studies is a very good option because there you will get interesting ways to learn the difficult topics. Mathematics is one of the most difficult subjects for most of the students. And this software makes the learning fun and makes students understand difficult questions in the very easy way. This software is easy to use, and the answer and explanations they provide are accurate and exact. Therefore if you are weak in mathematics, then you must take help of this software. It has many benefits and here are few of them.

The Benefits of using math software to solve polynomial expressions-

• Accuracy- software is well programmed, and hence it can accurately solve any mathematical questions. You can rely on its answer and if you have doubt then compare the solutions provided by the teacher.
• Solve any problem– online math software can answer any questions like algebra, HCF, LCM, polynomials, matrices, etc. Students can answer any topic of mathematics with accuracy using this software.
• Anytime- your teacher can’t help you every time. Once you reach home and you do not have any elder person to assist you in mathematics then this software can help you.

Online math software is thus very useful for students who have opted mathematics stream to solve simple polynomials problems form tough ones.